intervalos de confianza

En estadística, se llama intervalo de confianza a un par o varios pares de números entre los cuales se estima que estará cierto valor desconocido con un determinado nivel de confianza. Formalmente, estos números determinan un intervalo, que se calcula a partir de datos de una muestra, y el valor desconocido es un parámetro poblacional. El nivel de confianza representa el porcentaje de intervalos que tomados de 100 muestras independientes distintas contienen en realidad el valor desconocido. En estas circunstancias, α es el llamado error aleatorio o nivel de significación, esto es, el número de intervalos sobre 100 que no contienen el valor¹​

El nivel de confianza y la amplitud del intervalo varían conjuntamente, de forma que un intervalo más amplio tendrá más probabilidad de acierto (mayor nivel de confianza), mientras que para un intervalo más pequeño, que ofrece una estimación más precisa, aumenta su probabilidad de error.

Para la construcción de un determinado intervalo de confianza es necesario conocer la distribución teórica que sigue el parámetro a estimar, θ.²​ Es habitual que el parámetro presente una distribución normal. También pueden construirse intervalos de confianza con la desigualdad de Chebyshev.

En definitiva, un intervalo de confianza al 1 - α por ciento para la estimación de un parámetro poblacional θ que sigue una determinada distribución de probabilidad, es una expresión del tipo [θ₁, θ₂] tal que P[θ₁ ≤ θ ≤ θ₂] = 1 - α, donde P es la función de distribución de probabilidad de θ.

Índice

• 1Ejemplos
  • 1.1Intervalo de confianza de la media de una población
  • 1.2Intervalo de confianza de una proporción
  • 1.3Ejemplo práctico
• 2Véase también
• 3Referencias
  • 3.1Bibliografía

Ejemplos[editar]

Intervalo de confianza de la media de una población[editar]

De una población de media ${\displaystyle \mu }$ y desviación típica ${\displaystyle \sigma }$ se pueden tomar muestras de ${\displaystyle n}$ elementos. Cada una de estas muestras tiene a su vez una media. Se puede demostrar que la media de todas las medias muestrales coincide con la media poblacional:³​ ${\displaystyle \mu _{\bar {x}}=\mu }$

Pero además, si el tamaño de las muestras es lo suficientemente grande,⁴​ o la distribución poblacional es normal, la distribución de medias muestrales es, prácticamente, una distribución normal (o gaussiana) con media μ y una desviación típica dada por la siguiente expresión: ${\displaystyle \sigma _{\bar {x}}={\frac {\sigma }{\sqrt {n}}}}$. Esto se representa como sigue: ${\displaystyle {\bar {X}}\sim N(\mu ,{\frac {\sigma }{\sqrt {n}}})}$. Si estandarizamos, se sigue que: ${\displaystyle {\frac {{\bar {X}}-\mu }{\frac {\sigma }{\sqrt {n}}}}=Z\sim N(0,1)}$

En una distribución Z ~ N(0, 1) puede calcularse fácilmente un intervalo dentro del cual caigan un determinado porcentaje de las observaciones, esto es, es sencillo hallar z₁ y z₂ tales que P[z₁ ≤ z ≤ z₂] = 1 - α, donde (1 - α)·100 es el porcentaje deseado (véase el uso de las tablas en una distribución normal).

En esta distribución normal de medias se puede calcular el intervalo de confianza donde se encontrará la media poblacional si solo se conoce una media muestral (${\displaystyle {\bar {x}}}$), con una confianza determinada. Habitualmente se manejan valores de confianza del 95 y del 99 por ciento. A este valor se le llamará ${\displaystyle 1-\alpha }$ (debido a que ${\displaystyle \alpha }$ es el error que se cometerá, un término opuesto).

Para ello se necesita calcular el punto ${\displaystyle X_{\alpha /2}}$ —o, mejor dicho, su versión estandarizada ${\displaystyle Z_{\alpha /2}}$ o valor crítico— junto con su "opuesto en la distribución" ${\displaystyle X_{-\alpha /2}}$. Estos puntos delimitan la probabilidad para el intervalo, como se muestra en la siguiente imagen:

Dicho punto es el número tal que:

${\displaystyle \mathbb {P} [{\bar {x}}\geq X_{\alpha /2}]=\mathbb {P} [z\geq z_{\alpha /2}]=\alpha /2}$

Y en la versión estandarizada se cumple que:

${\displaystyle z_{-\alpha /2}=-z_{\alpha /2}}$

Así:

${\displaystyle \mathbb {P} \left[{\bar {x}}-z_{\alpha /2}{\frac {\sigma }{\sqrt {n}}}\leq \mu \leq {\bar {x}}+z_{\alpha /2}{\frac {\sigma }{\sqrt {n}}}\right]=1-\alpha }$

De lo cual se obtendrá el intervalo de confianza:

${\displaystyle ({\bar {x}}-z_{\alpha /2}{\frac {\sigma }{\sqrt {n}}},{\bar {x}}+z_{\alpha /2}{\frac {\sigma }{\sqrt {n}}})}$

Obsérvese que el intervalo de confianza viene dado por la media muestral ${\displaystyle ({\bar {x}})}$ ± el producto del valor crítico ${\displaystyle Z_{\alpha /2}}$ por el error estándar ${\displaystyle ({\frac {\sigma }{\sqrt {n}}})}$.

Si no se conoce y n es grande (habitualmente se toma n ≥ 30):⁵​

Aproximaciones para el valor ${\displaystyle z_{\alpha /2}}$ para los niveles de confianza estándar son 1,96 para ${\displaystyle 1-\alpha =95\%}$ y 2,576 para ${\displaystyle 1-\alpha =99\%}$.⁶​

Intervalo de confianza de una proporción[editar]

El intervalo de confianza para estimar una proporción p, conocida como una proporción muestral p_n de una muestra de tamaño n, a un nivel de confianza del (1-α)·100% es:

${\displaystyle (p_{n}-z_{\alpha /2}{\sqrt {\frac {p_{n}(1-p_{n})}{n}}},\;p_{n}+z_{\alpha /2}{\sqrt {\frac {p_{n}(1-p_{n})}{n}}})}$

En la demostración de estas fórmulas están involucrados el Teorema Central del Límite y la aproximación de una binomial por una normal.⁷​

Ejemplo práctico[editar]

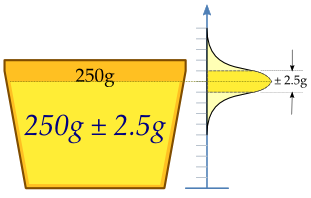
Una máquina llena tazas con helado, y se supone que está ajustada para verter la cantidad de 250 g. Como la máquina no puede llenar cada taza con exactamente 250 g, el contenido que se añade a cada taza individual presenta cierta variación y se le asigna una variable aleatoria X. Se asume que esta variación se ajusta a una distribución normal de alrededor de la cantidad promedio deseada de 250 g, con una desviación estándar de 2.5 g.

Para determinar si la máquina está adecuadamente calibrada, se toma una muestra aleatoria de n = 25 tazas de helado para pesarlas. La medición resultante es X₁, ..., X₂₅, una muestra aleatoria procedente de  X.

Para μ, es suficiente con dar una estimación. El estimador adecuado es la media muestral:

${\displaystyle {\hat {\mu }}={\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}.}$

La muestra señala los pesos reales x₁, ..., x₂₅, con media:

${\displaystyle {\bar {x}}={\frac {1}{25}}\sum _{i=1}^{25}x_{i}=250.2\,{\text{gramos}}.}$